Abstract
In the realm of Mars robotics exploration, the groundbreaking Mid-Air Helicopter Delivery (MAHD) mission concept represents a paradigm shift in Entry, Descent, and Landing (EDL), introducing a revolutionary approach to deploy drones on the Red Planet. Unlike its predecessors, MAHD leverages a jetpack to decelerate the Mars Science Helicopter (MSH) after separation from the backshell, allowing it to achieve the ideal conditions for helicopter take-off in mid air. While the MAHD mission concept promises significant benefits, including cost reduction, access to challenging terrains, and increased payload capacity, its ambitious goals also give rise to a distinct set of challenges, particularly within the domain of monocular visual-odometry frameworks employed for the navigation of these technologies.
In this work, we conduct an extensive analysis of the range-VIO method under the challenging conditions of MAHD. The investigation takes place in a custom simulation environment designed to replicate the intricate complexities of Mars landscapes, including rough terrain with steep elevation slopes and high-altitude trajectories starting at 12 kilometers above the Martian surface. The findings from our study reveal a critical limitation in the existing range-VIO approach, particularly when applied to high altitudes and on highly non-planar terrains, where the assumption of local planarity becomes significantly violated, leading to performance degradation. To address this issue, we propose an innovative alternative to the range-VIO method that eliminates the need for any type of ground planarity assumption, making it adaptable to any terrain structure, while still being able to observe scale and mitigate error drift under constant-velocity motion and without relying on prior maps. We provide a robust evaluation of this novel implementation, demonstrating its effectiveness in a realistic simulation environment. By conducting exhaustive assessments using flight data representative of MAHD's scenarios, we highlight the potential benefits and enhanced performance of this new approach, paving the way for more adaptable and efficient navigation systems in the context of Mars exploration.
Mid-Air Helicopter Delivery (MAHD) on Mars
In the context of navigation, the main objective is to precisely control the jetpack's velocity, maintaining it within the tight boundaries of 1 m/s. This critical phase of navigation begins after heatshield separation, typically occurring at an altitude of around 12 kilometers above the Martian surface. Here, terrain-relative navigation comes into play, providing essential positional accuracy.
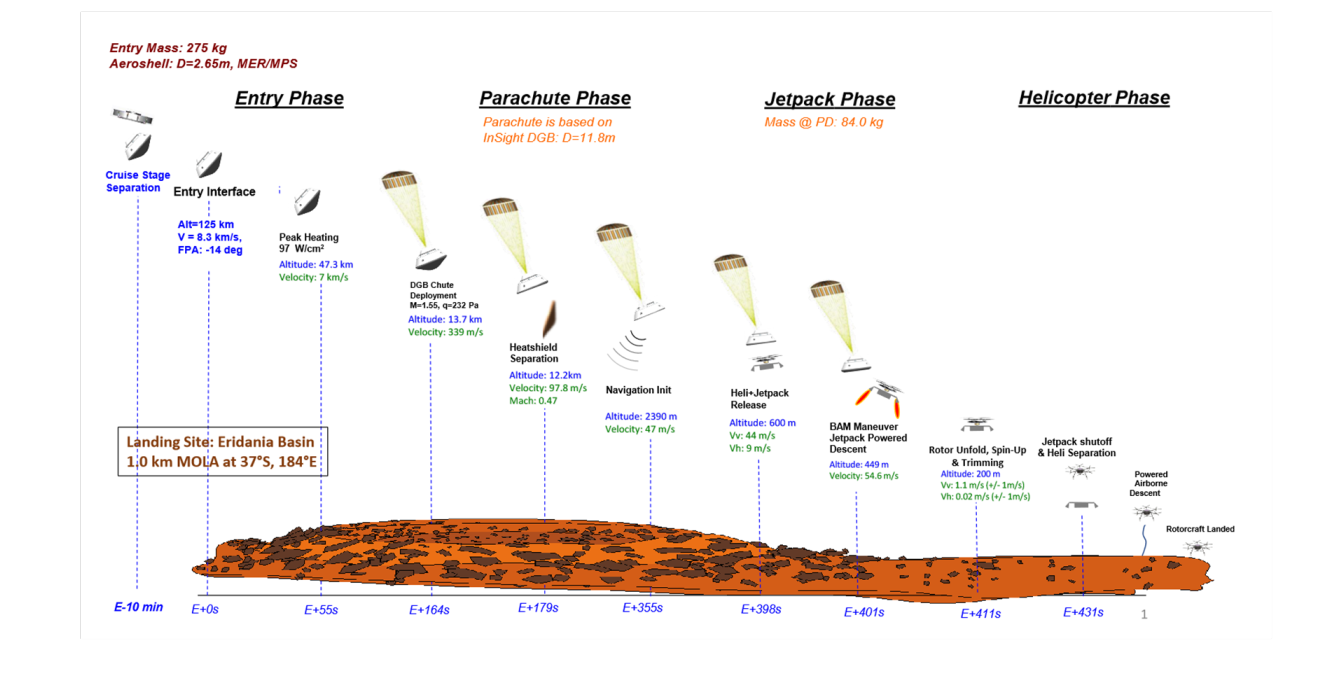
MAHD introduces a range of compelling advantages when compared to conventional EDL approaches. One of the standout features of MAHD is the absence of a lander. Unlike the Mars 2020 mission, which relies on the sky-crane to execute the descent, MAHD optimizes the available space within the aeroshell for larger rotorcraft. This elimination of the lander represents a significant cost reduction, making missions more economically feasible. In addition to that, MAHD simplifies the EDL system, reducing mission complexity and associated costs substantially. The streamlined architecture enhances efficiency and reliability during the critical descent and landing phases. Lastly, building upon the success of the Mars Science Helicopter, MAHD extends the reach of exploration by providing access to hazardous and higher-elevation terrains on Mars and therefore opening up new possibilities for scientific investigation. These advantages position MAHD as a highly promising EDL solution for Mars missions, particularly those focused on helicopter-only endeavors, such as the Mars Science Helicopter. MAHD not only enhances cost-effectiveness and mission feasibility but also broadens the horizons of Martian exploration by venturing into challenging terrains that were once out of reach.
Problem statement and main challenges
In the context of navigation, the main objective is to precisely control the jetpack's velocity, maintaining it within the tight boundaries of 1 m/s. This critical phase of navigation begins after heatshield separation, typically occurring at an altitude of around 12 kilometers above the Martian surface. Here, terrain-relative navigation comes into play, providing essential positional accuracy. During this descent phase, the primary focus is on accurately estimating the vehicle's velocity, a pivotal factor for both the safe landing and the subsequent control of the jetpack in the final stages of descent. To meet the stringent mission specifications, the navigation system aims to provide velocity estimates well within the 3σ bounds of 1 m/s. This level of precision is indispensable for maintaining a stable hover and facilitating a secure transition to powered flight.
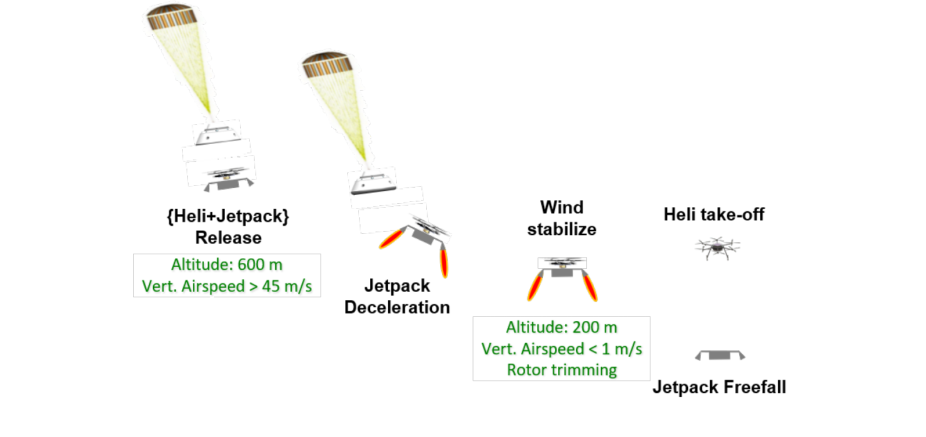
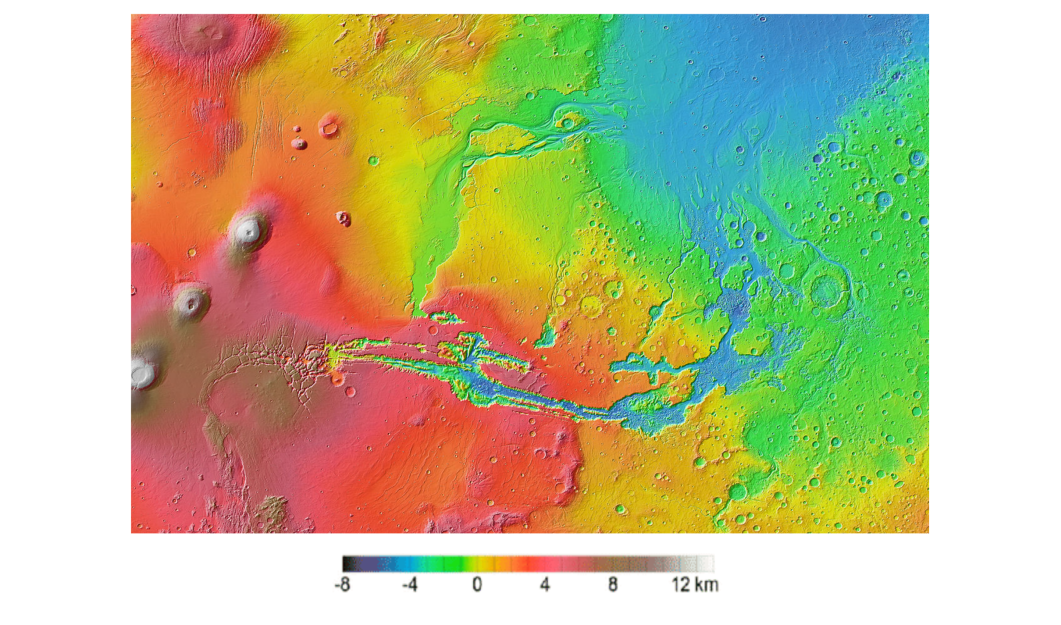
The navigation challenges of the Mars Science Helicopter are multifaceted and intricate. First and foremost, navigating over the highly non-planar Martian terrain, exemplified by regions like Valles Marineris with its substantial altitude variations of ±4 km, as it is shown in Figure 1.6, demands a navigation system that can swiftly adapt to changes in altitude and negotiate the rugged landscape effectively. Secondly, the initialization of the state estimator under the uncertain and demanding conditions of MAHD is a critical concern. The prior knowledge of the helicopter's state may not suffice for achieving convergence and precise state estimation during descent, necessitating the potential implementation of an independent initialization module for the Kalman Filter. Furthermore, MAHD encounters phases of constant velocity motion, particularly during the parachute and jetpack terrain-relative hover phases 1 . The constant velocity motion in the latter two phases poses challenges for motion estimation, as it lacks the IMU sensor excitations observed in more dynamic maneuvers. To address this, integrating additional sensors like altimeters becomes imperative to disambiguate scale information. Lastly, MAHD conducts terrain-relative navigation without access to prior maps of the Martian surface. Instead, it relies on continuous comparisons of sensor data with observed terrain features in real-time. While this approach enables the system to determine its position and orientation relative to the local terrain, it cannot correct x and y position errors in an absolute sense, only relative to the initial guess fed into the state estimation framework.
Representative Mars Simulation Environment Development
One of the contributions of this work lies in the development of a highly sophisticated and comprehensive simulation environment tailored specifically for Mid-Air Helicopter Delivery operations on Mars. The importance of such a simulation environment cannot be overstated, as it serves as a fundamental tool for advancing our understanding in this unique and challenging field of planetary exploration.

In order to achieve the highest level of precision in the novel simulation environment, we use Digital Terrain Models (DTMs) of various Martian sites sourced from the High-Resolution Imaging Science Experiment (HiRISE) website. HiRISE data are derived from measurements taken by an orbiting spacecraft equipped with a powerful camera capable of capturing images covering extensive Martian terrain while discerning features with a resolution of about 1 meter. The complete functionality of the proposed hybrid simulator is achieved through a series of key steps. Firstly, we have seamlessly integrated an external trajectory generator package with Unity, namely the Robotics Toolbox package, allowing us to dynamically control the drone's position and orientation within the rendering engine over time. IMU data generation is then carried out offline, synchronized with the input trajectory provided to the rendering engine. For image generation, we make use of pre-existing pinhole camera models within Unity, configured to have a downward perspective, and Airsim is employed through an existing Python API for image capture. Additionally, we have implemented a C# model for an altimeter sensor, emulating a downward-facing 1D-LRF, which employs ray-tracing techniques on the rendered 3D model to determine the distance between the drone and the ground. To manage the altimeter data collected from Unity, we have developed a dedicated Python API.

Online feature initialization with 1D-LRF measurements
The primary contribution of this thesis revolves around the integration of 1D Laser Range Finder measurements into the visual-odometry framework employed by the Mars Science Helicopter, denoted as xVIO. What sets this method apart is its capacity to perform this integration without necessitating any assumptions regarding the terrain's planarity.
Selection criteria for range-based features
Before adding a range-feature to the SLAM tracks for the visual update, we have to make sure that the feature represents a corner and that it can be tracked over time. In order to determine that, we make use of the minimum eigenvalue score metrics that computes the minimum eigenvalue of the spatial gradient matrix. A new range-feature is determined when both of the following conditions are satisfied:
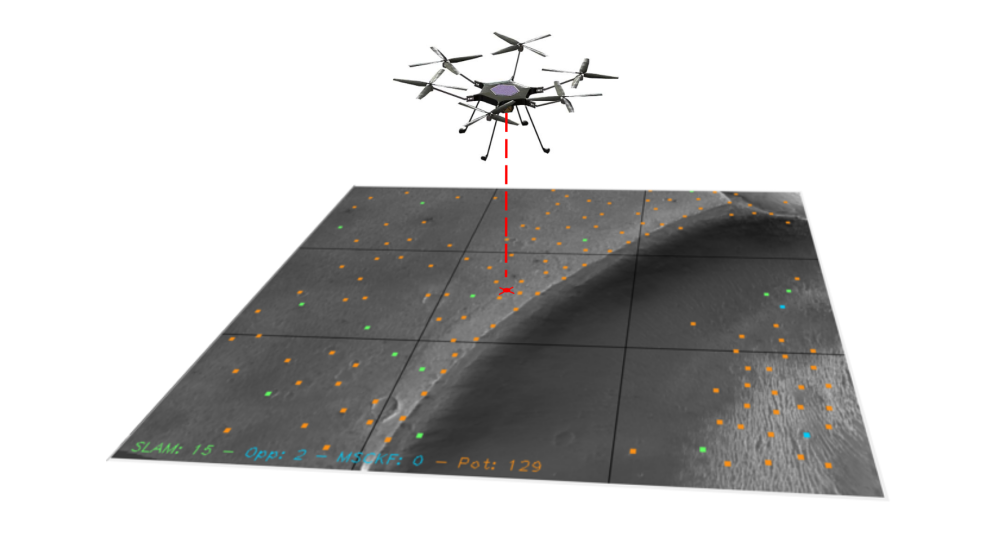
Range-features initialization
Once a pixel satisfies the conditions elucidated in the preceding section, it becomes a candidate for inclusion in the feature matches and subsequently undergoes tracking, following a protocol similar to that of any other SLAM feature. As it persists in being tracked for a duration exceeding the minimum track length parameter specified at run-time, it attains eligibility for inclusion in the set of SLAM tracks used for updates. What sets it apart from the other SLAM tracks is the intentional effort to guarantee the inclusion of the range-feature within these tracks, and additionally the way these features are initialized. Once the range feature has been added to the SLAM tracks, the update rule for that feature follows the same pattern of any other SLAM feature.
xVIO demo with range-features initialization (red: ranged-features, green: normal SLAM features):
Results
Scale observability with range-feature initialization
The primary objective of range-feature initialization revolves around testing the algorithm's effectiveness for scale observability. The trajectory employed for evaluation purposes takes a simpler form, characterized by a horizontal path featuring a velocity vector of [50, 0, 0] m/s, staying the whole time at an elevation of 12 km above a uniformly flat terrain. The sequence is analyzed within the same analytical framework as previously described, although with the introduction of initial condition errors. Specifically, a 20% error is imposed upon the initial position, contributing to a perturbation in the scale aspect of the feature plane. Additionally, a 20% error is applied to the norm of the velocity vector, thereby establishing an overall scale error of 20%. With particular focus on the x-axis, representing the principal direction of motion, the results illustrated by the plots are noteworthy. In the absence of range-feature initialization, the scale factor remains unobserved.
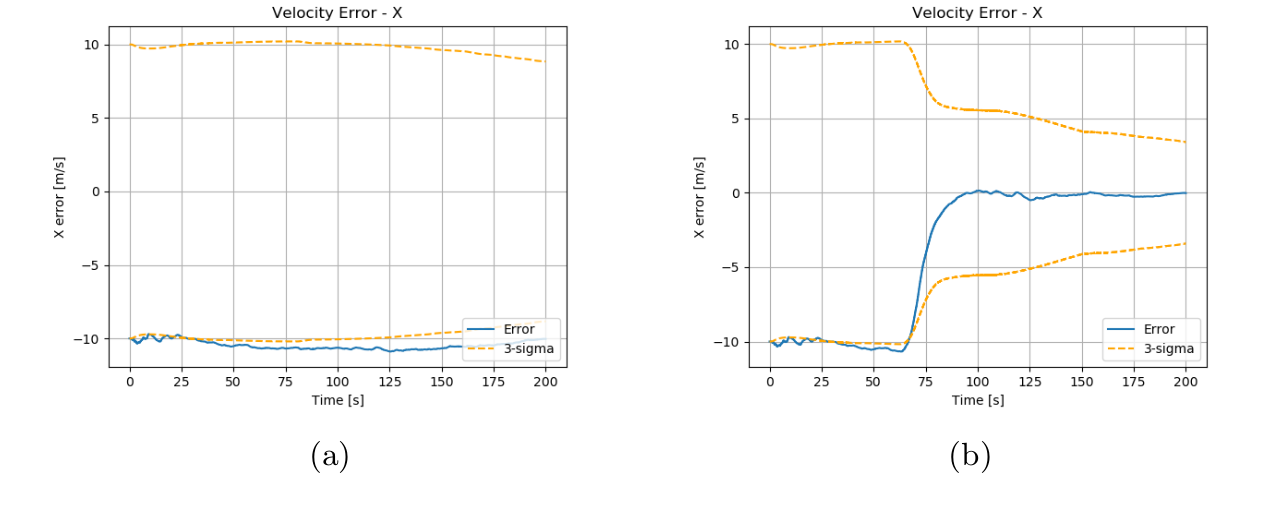
(a) without ranged-feature initialization (b) with ranged-feature initialization
Improved performance on MAHD trajectories
This section serves as a more in-depth assessment within a single MAHD-like sequence, aiming to highlight the impact of range-feature initialization. The primary focus is on the velocity error along the z-axis, with a specific interest in observing the effectiveness of range-feature initialization in mitigating drift. In the trajectory under consideration, different from the one showcased before, the true velocity of the drone is [−10, −1, −55] m/s, and the trajectory covers a range from 12 kilometers down to 200 meters. The true effectiveness of the novel algorithm becomes more apparent when dealing with the inherent randomness and complexities of MAHD. In this case, while comparing the vision-only method to the one with range-features, we observe a divergence behavior in the velocity along the z-axis for the vision-only method. In contrast, the range-features initialization approach consistently keeps the error close to zero throughout the entire sequence. This outcome serves as another validation of the effectiveness of the implemented method in challenging MAHD scenarios. Deploying the range-feature initialization method allows us to reduce the final 3σ bound on the velocity from [1.613, 1.707, 3.653] m/s to [1.115, 0.983, 0.608] m/s.
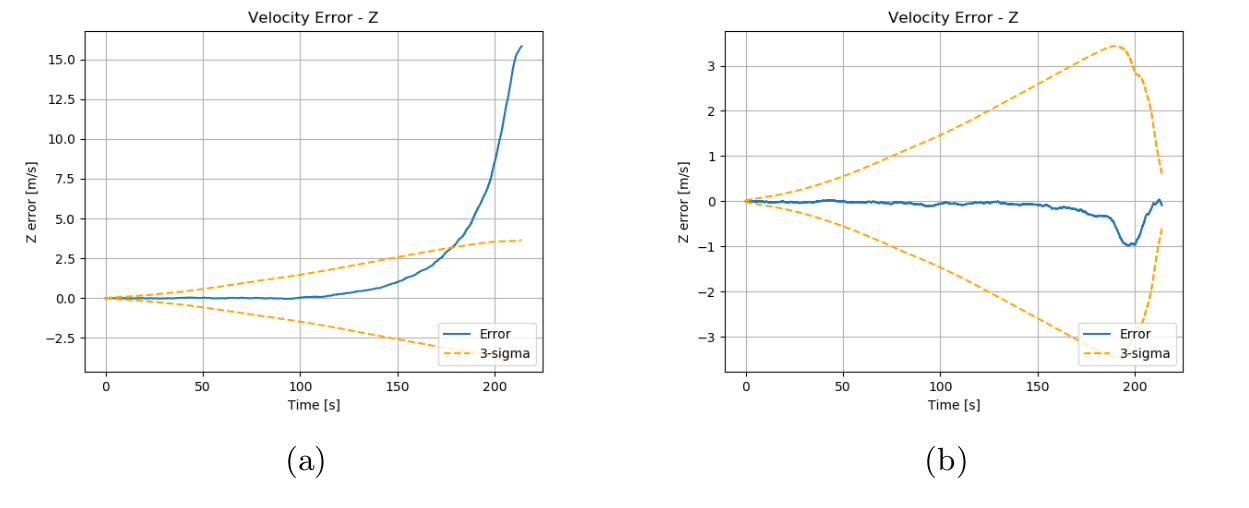
(a) without ranged-feature initialization (b) with ranged-feature initialization